Build Your Own Glockenspiel
The glockenspiel is an idiophone instrument, meaning that it produces sound by vibrating the substance of the instrument itself. This is notably different from wind instruments, which produce sound by shaping a column of air inside a tube; as well as string instruments, which produce sound through vibrations of strings. Glockenspiels usually have metal slabs, but we will be examining metal tubes since that’s what we used.
The Three Modes of Vibration
Metallic tubing has three different vibrational modes that can be excited – two of them are harmonic in nature, while one is non-harmonic. The torsional and longitudinal modes of vibration are harmonic, however they are not excited during playing. The only vibrational mode that is excited during play is the transverse mode, which is non-harmonic. Thus, metallic tubes will produce audible frequencies that are not clear and distinct pitches, and its overtones will not conform to the harmonic series. The purest tone that can be heard would be two pitches approximately 17.5 semitones apart.
The transverse vibrational mode deforms the tube in an up and down motion, resembling a sinusoidal wave. Torsional vibrations are characterized by a twisting of the tube in a diagonal or side-to-side motion. Finally, in the the longitudinal mode, the energy of the wave travels through the bar instead of having it displace air.
The Strike
Upon being struck by a mallet, a metal tube vibrates in a transverse motion. Unlike aerophones, the audible sound is not being produced by a vibrating column of air, but rather the deformation of the tube itself. When the tube is struck at the midpoint, it vibrates in a transverse wave in its fundamental mode. Because the ends are free, the tube vibrates with two nodal points and three antinodal points. The area where the mallet strikes the tube becomes an
antinode along with the two ends. The antinodal points are the areas of greatest movement, and the nodal points are where no movement occurs. Nodal points are areas with an amplitude of vibration equal to zero. These areas of no vibration, or nodes, are precisely where the supports for the glockenspiel are placed. By making contact with the tube at these points, the supports serve to dampen all other modes of vibration except the fundamental mode. As shown in the diagram, when the tube deforms up and down, a longitudinal wave is produced outside the tube in the surrounding air. When the tube bends upwards a compression is formed above the tube, and when it bends downward a rarefaction is formed above the tube. As a result of this vibration, longitudinal waves radiate outward in a circular fashion both above and below the tube.
Frequency
Frequency is mathematical representation of how low or high a pitch is, and is based on the rate at which waves vibrate. It is measured in Hertz, or number of complete wave cycles per second, and is commonly abbreviated as Hz. Since sound is produced by the vibrating tube itself, the amount of time it takes for one complete up and down transverse motion, will determine the tube's frequency. The frequency of a tube can be derived by the following equation, where L is the tube length:
Frequency = 1/L2
Nodal Points
The nodal points for the first three modes of vibration are displayed in the wavelength graphic.
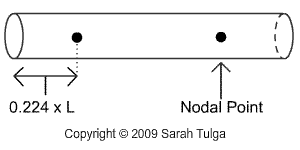
These nodes are important reference points to consider when designing and constructing a glockenspiel. Most importantly, are the nodal points for the fundamental mode, which produces the lowest resonant frequency that is possible for a given tube. As shown, the nodal points for the fundamental mode are at 0.224 x L, where L is equal to the total length of the tube.
It is important that the supports for your glockenspiel are directly under these points – this also applies to holes that are drilled into chimes for hanging purposes. The first mode of vibration is not affected or dampened at these points, because these points are at nodal positions, which by definition have a vibrational amplitude equal to zero. The second and third modes, as shown in the wavelength graphic, have large vibrational amplitudes at these support points, and are consequentially silenced or dampened. By allowing a tube to freely resonate the fundamental mode, while dampening higher modes, the overall sound and pitch of the tube becomes more predictable.